Ya he escrito varias entradas del sistema electoral español para repartir los escaños. Ahora con un nuevo actor, VOX, que también parece que va a participar en el reparto de los escaños y un PP bastante debilitado. Veremos el reparto final, pero el sistema puede dar lugar a interesantes carambolas.
Con el sistema de reparto D’Hondt se puede calcular fácilmente el número de votos que aseguran a un partido alcanzar un escaño seguro, que es el cociente obtenido al dividir el número de votos totales a las candidaturas por el número de escaños a repartir más uno (el número de votos debería ser mayor que este cociente). Luego hay que ver si este número es menor que el umbral del 3 % de votos válidos (votos a candidaturas más votos en blanco) que se exige a un partido para participar en el reparto provincial, que solo afecta a las provincias de Madrid y Barcelona.
Si se quiere afinar más, para calcular el porcentaje de voto habría que hacer suposiciones sobre cuánto porcentaje de voto en blanco va a haber y de las candidaturas que no van a llegar a posibilidades de tener un escaño por sus pocos votos (menos del 3 %). Luego habría que saber cuántas candidaturas realmente son competitivas en la provincia, porque a la hora del reparto, cuantas más candidaturas, es más fácil que haya votos de sobra de la candidatura, que si los votantes se hubieran quedado en casa, no hubiera cambiado el reparto. Haciendo simulaciones de andar por casa, centrados en los casos más interesantes de provincias que repartan alrededor de 4 escaños entre cuatro o más partidos, sale la siguiente fórmula aproximada, en porcentaje de voto válido:
ÚLTIMO_ESCAÑO = (100 – VOTOS_FUERA) / (N_DIPS + 0.43 * N_PARTIDOS – 0.42)
donde VOTOS_FUERA es la suma de votos en blanco y votos de partidos pequeños sin opciones, que de manera conservadora he estimado en 2 (% voto válido). N_DIPS es el número de diputados en la provincia y N_PARTIDOS el número de partidos con opciones de llegar a un escaño. Luego habría que corregir para el caso de provincias con pocos partidos competitivos, para que (0.43 * N_PARTIDOS – 0.42) dé al menos uno, que ya he comentado que siempre asegura un escaño. Y finalmente que el ÚLTIMO_ESCAÑO tiene que ser mayor del 3 % cuando estamos hablando del voto que necesita un partido, por la imposición del umbral.
Haciendo este ejercicio a las pasadas elecciones generales de 2016, este es el resultado:
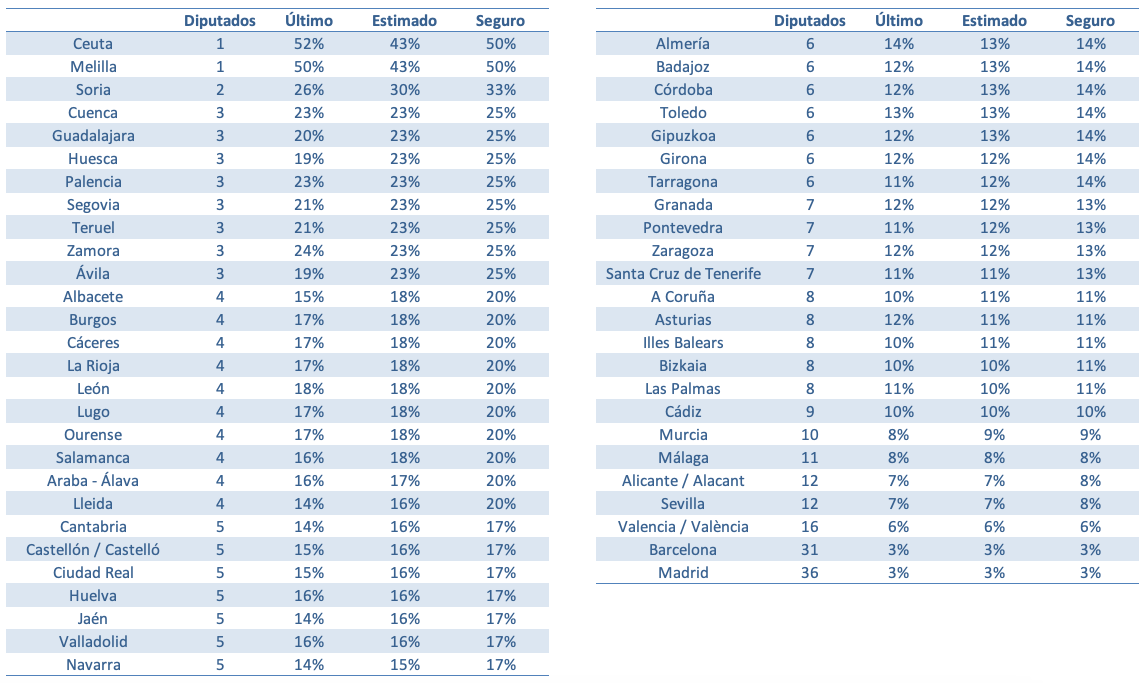
Donde la columna ÚLTIMO indica el coste del último escaño adjudicado (subiendo al 3 % si el valor es menor que el umbral); la columna ESTIMADO indica el valor del último escaño según el método indicado; y SEGURO es el primer cálculo indicado que asegura sí o sí un escaño. El número de partidos competitivos lo he considerado 6 para las provincias catalanas, 5 para las canarias, vascas y Navarra y 4 para el resto. Salvo para las circunscripciones que reparten 1 o 2 escaños, considero que la estimación es suficientemente buena.
Si hago el mismo ejercicio para 2019:
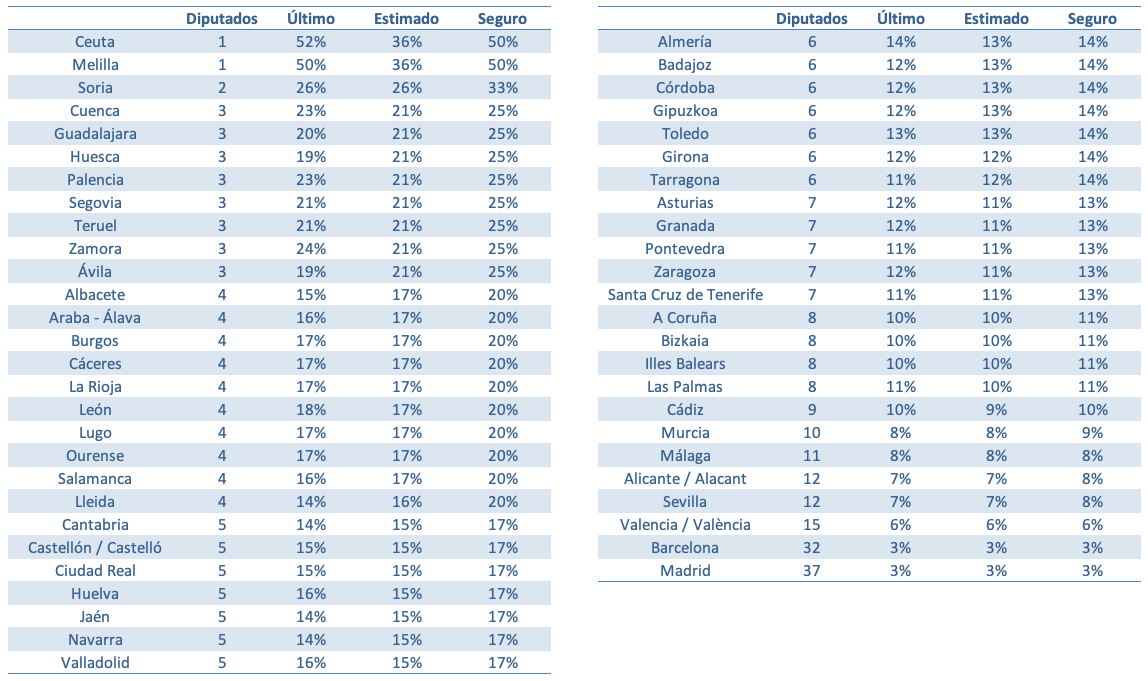
Donde ÚLTIMO sigue siendo la misma columna que 2016 para comparar con el resto de las columnas; he actualizado el número de escaños provinciales y ahora he considerado que el número de partidos competitivos es 6 para las provincias catalanas y canarias y 5 para el resto. A partir de esta tabla se puede hacer un gráfico que indica el porcentaje escaños de las provincias en las que un partido podría conseguir escaños con respecto a su votos:
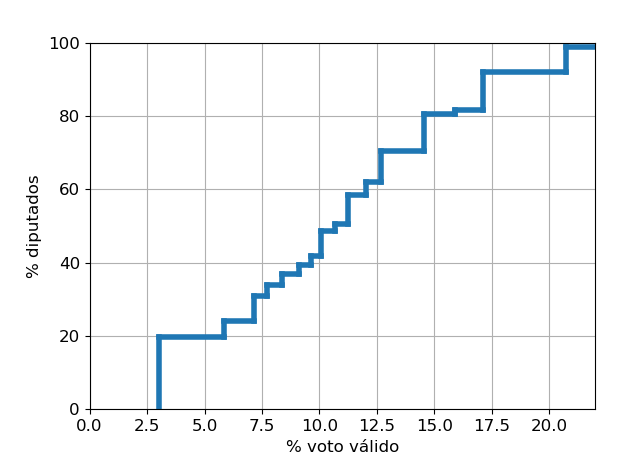
Así que un partido que saque menos votos del 10 % no tiene posibilidades de alcanzar un escaño en las provincias que reparten un 50 % de los escaños.
De esta gráfica, se puede estimar cuántos escaños conseguiría el partido nacional que quede en peor lugar en función de su voto, suponiendo para este ejercicio que el voto está repartido uniformemente por las provincias, su caso más desfavorable:
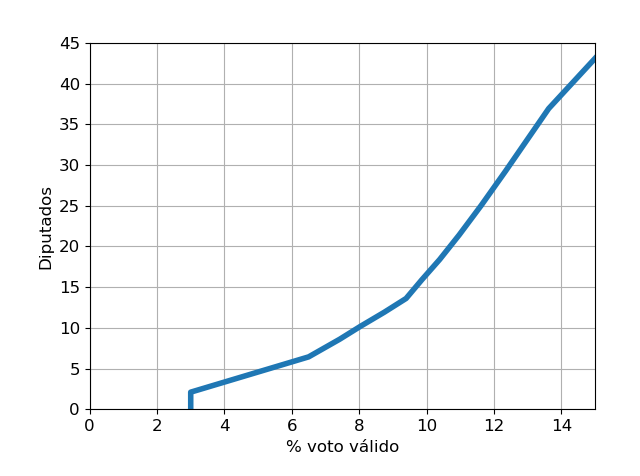
Un partido que no llegue al 10 %, va a rentabilizar malamente sus votos: un 10 % de los diputados son 35. Entre 10 y 15 %, su rendimiento mejora, pero sigue siendo malo. A partir del 15 % ya va a mejorar más, además que sea difícil que el último partido obtenga más del 15 %. Y es que lo que no rentabilice el último partido, seguro que lo rentabiliza el primero y segundo, pero también —según las circunstancias— el tercero y cuarto.
Por supuesto que esta gráfica puede variar bastante dependiendo de la localización de los votos: un partido que tenga el 25 % de los votos en las Castillas y Extremadura, aunque luego su promedio nacional baje bastante, va a rentabilizar y mucho sus votos.
