El modelo de Nate Silver para el mundial de fútbol consideraba que la selección francesa era el cuarto equipo con más probabilidades de ser campeón del mundo, con un 8 %, pero lejos del 19 % o 17 % que daba a Brasil o España. Además, de las cuatro selecciones más favoritas para ganar el mundial, solo una —Francia— llegó a semifinales. Visto así, no parecería que el modelo haya sido muy exitoso… ¿o sí? Pero, ¿cómo evaluarlo?
Hay muchas posibles formas de ver si las predicciones de un modelo han sido correctas o no. Pero tampoco hay que perder de vista que un modelo puede ser perfectamente correcto —en el sentido estadístico—, pero ser completamente inútil: por ejemplo, un modelo que en la fase eliminatoria pronostique que cada equipo tiene un 50 % de ganar, será perfectamente correcto al hacer el análisis global, pero será completamente inútil. Eso nos llevaría a otra pregunta clave para la evaluación de un modelo: ¿proporciona el modelo más información que la que podría pronosticar un aficionado «enteradillo»?
Volviendo al modelo de Nate Silver, una forma de evaluarlo es calcular, a partir de los porcentajes dados a priori, cuántas veces prevé acertar y cuántas lo hace realmente. Consideraré que el modelo acierta un resultado si coincide con la opción que da con mayor probabilidad. El gráfico que muestra los partidos acertados y fallados es este:
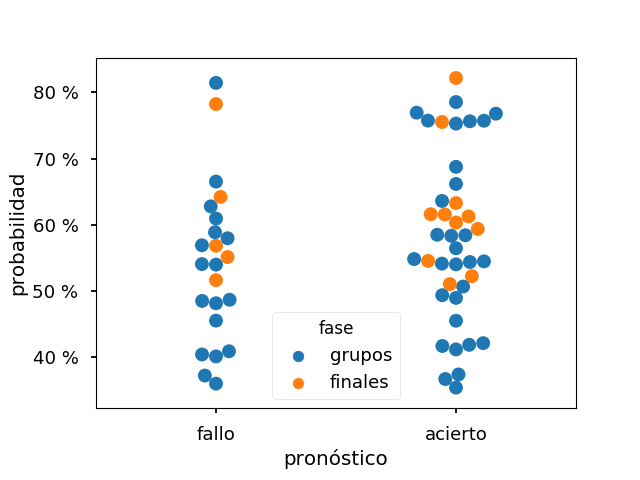
Así a primera vista si se ve que el modelo ha acertado más que fallado; que cuando la probabilidad de la opción es muy alta, > 70 %, hay bastantes más aciertos que fallos; pero que cuando la probabilidad de fallo es baja, < 40 %, tampoco es que el modelo falle excesivamente. Como curiosidad, consideradas las previsiones de esta forma, el modelo no pronosticaba ningún empate en la fase de grupos.
Si se hacen los cálculos, el número de aciertos esperados a priori es de 36.3. Sin embargo, los aciertos reales son 41 (de 64 partidos), algunos más. Y esta es la distribución esperada (la línea naranja, los aciertos esperados; la línea verde, los aciertos reales; y las áreas sombreadas, las colas de la distribución, que cubran hasta 2.5 % por cada lado):

Así que globalmente, si el modelo fuera correcto, tenía previsto, como valor esperado, acertar el 57 % de los partidos, pero acertó el 64 % de los partidos, que aunque algo más, no está en la cola de la distribución. De forma más amplia, el modelo se podría considerar correcto si acertaría entre el 45-70 %.
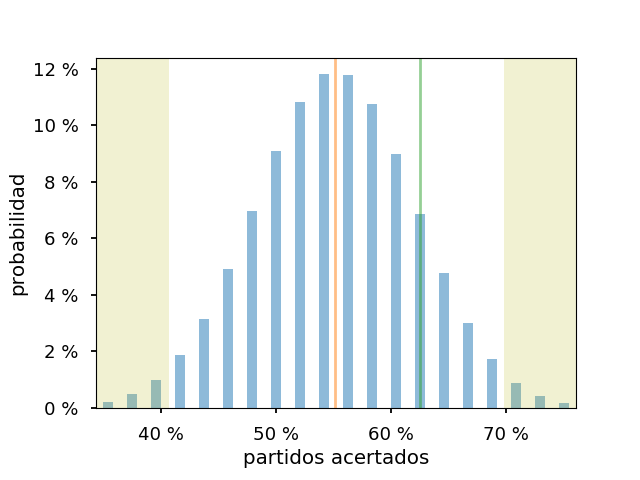
Si, aún a costa de reducir la precisión, se calculan los gráficos para la fase de grupos (48 partidos, 26.4 aciertos esperados, 30 acertados):
Y la fase eliminatoria (16 partidos, 9.9 aciertos esperados, 11 aciertos):
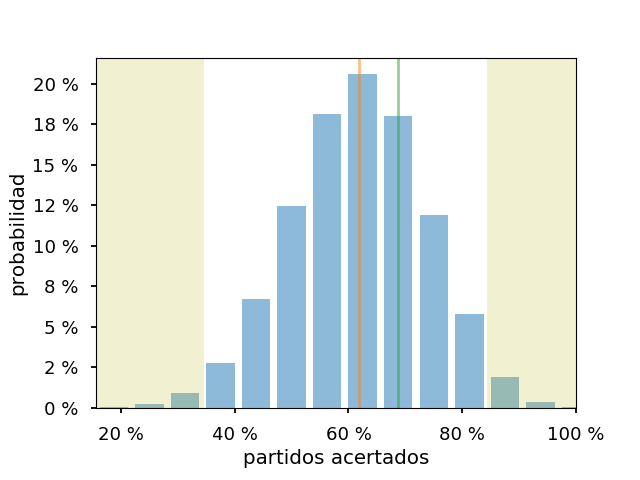
Así que considerando cada partido, el modelo parece ser bastante correcto, con un número de aciertos mayor que el valor esperado promedio. Pero con unos «rangos de corrección» bastante amplios.
Pero también vemos que con el modelo no vamos a esperar acertar el resultado del 30 % de los partidos; o que nos asegure que el modelo va ser útil para acertar determinado partido, aún con probabilidades del 80 %, sino que es correcto globalmente.
Otra evaluación que se puede hacer es ver si el modelo es correcto en los equipos que van a llegar a semifinales o cuartos, y cuántos equipos esperarían acertar.
El gráfico donde se ven hasta dónde ha llegado cada equipo con respecto a las probabilidades previstas por el modelo, es este:

Y el mismo gráfico con la probabilidad en escala logarítmica:
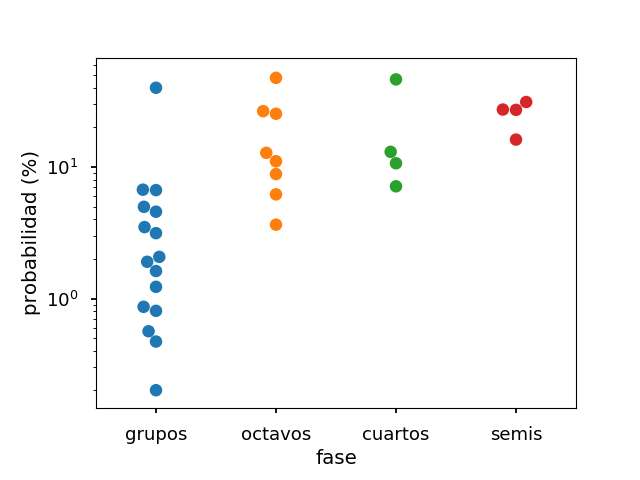
Se observa que los equipos con probabilidad más baja de llegar a semis, no pasan a octavos; que los equipos que llegan a semis no tenían la máxima probabilidad, pero sí estaban por la parte alta; y que los tres equipos con máxima probabilidad han caído en otras fases.
Para hacer los cálculos de probabilidad de llegar, he ido dividiendo en grupos de diferentes tamaño (Del 1-4, 1-6, 1-8, etc) e ir viendo el valor promedio esperado del número de equipos que llegarían a semis, comparando con el valor real y la distribución de valores posibles. El cálculo de la distribución no es formalmente correcta, ya que no hay suficientes datos. Sin embargo comprobé que calculando el promedio de dos distribuciones, el valor esperado es muy similar al que tendría que ser. La primera distribución es calcular todas las combinaciones posibles de semifinalistas, y dar a cada combinación de los elementos una determinada probabilidad: por ejemplo si los semifinalistas son 1, 2, 3 y 4, su probabilidad sería P1 × P2 × P3 × P4, donde P1 es la probabilidad del elemento 1 de llegar a semis. Y para terminar, normalizar por la suma de todas las probabilidades. La segunda distribución se construye de forma similar, pero para la combinación de semis de 1, 2, 3 y 4 se asigna una probabilidad de P1 × P2 × P3 × P4 × (1 – P5) × (1 – P6) × ··· × (1 – P32). La primera distribución subestima el valor promedio esperado y la segundo lo sobrestima, dando el promedio de ambas distribuciones un valor bastante próximo, por lo que considero que la distribución obtenida con el promedio de las dos es aceptable para la comparación.
Así, para los cuatro equipos con más probabilidades de llegar a semis, este el gráfico de la comparación:
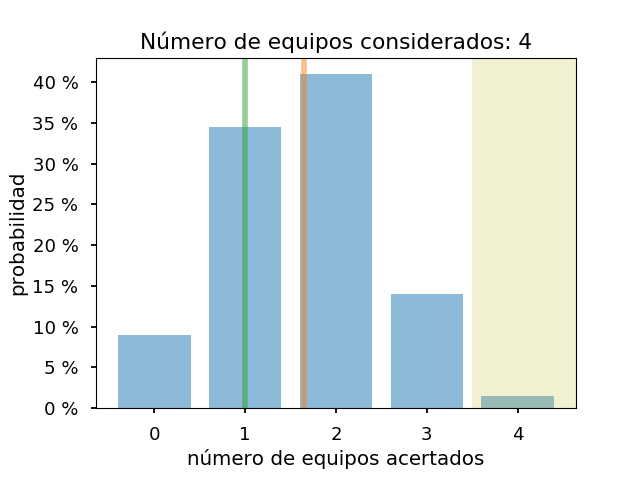
El valor esperado es de 1.6 equipos de los cuatro en semis (línea naranja) y uno (Francia), acertado (línea verde). Como vemos, solo el caso de que los cuatro equipos fueran los correctos sería el que cuestionaría más el modelo, ya que da una probabilidad muy baja para ese caso.
Para el caso de considerar de cuántos equipos de los seis con más probabilidades llegarían a semis, este es el gráfico:

Y los gráficos para los 8, 12 y 16 equipos con más probabilidades:
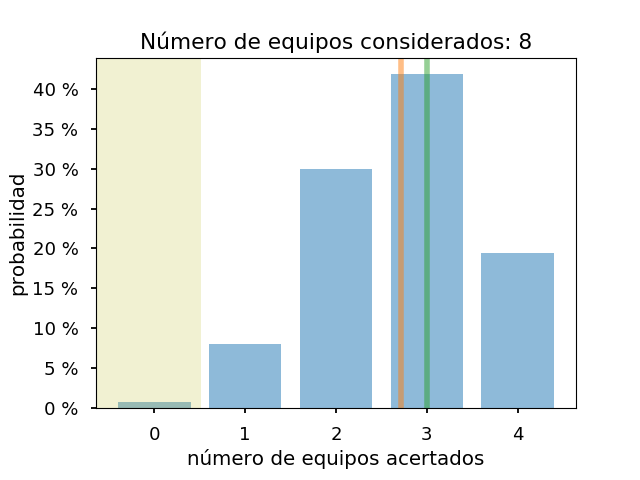

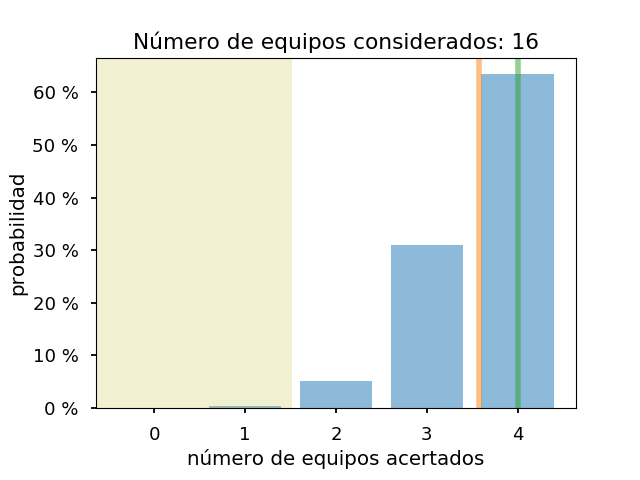
Como se ve, para asegurarse de llegar a acertar un equipo de semis, habría que considerar al menos los doce equipos con más probabilidades, si el modelo es correcto. Y con 16, no se puede descartar que solo se estén acertando dos equipos de semis. También, salvo el caso de cuatro equipos, el resultado real es mejor que el previsto.
Si se hace el mismo ejercicio para todas las combinaciones de octavos posibles:
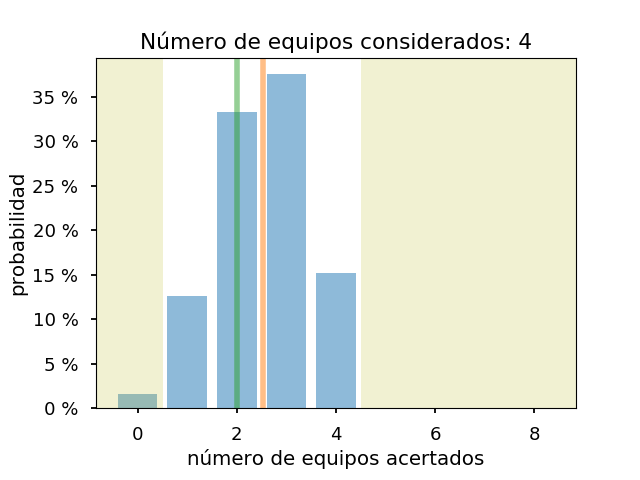

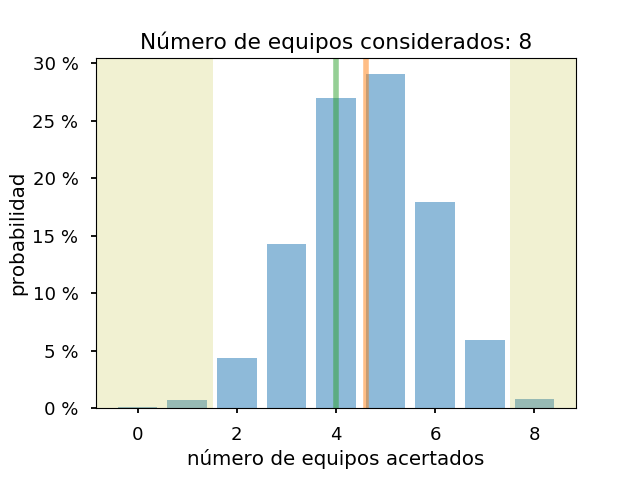
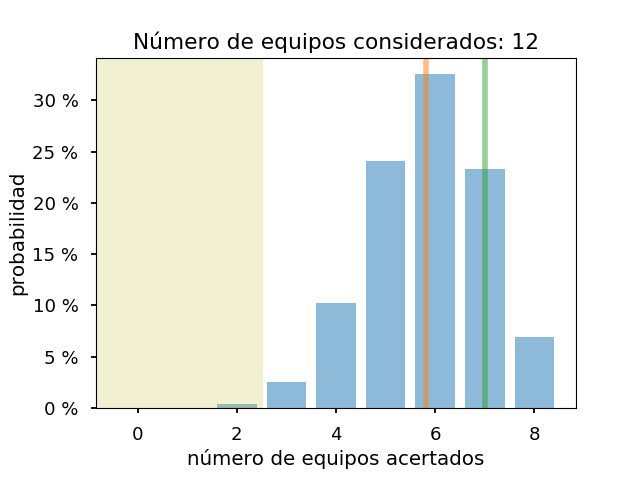
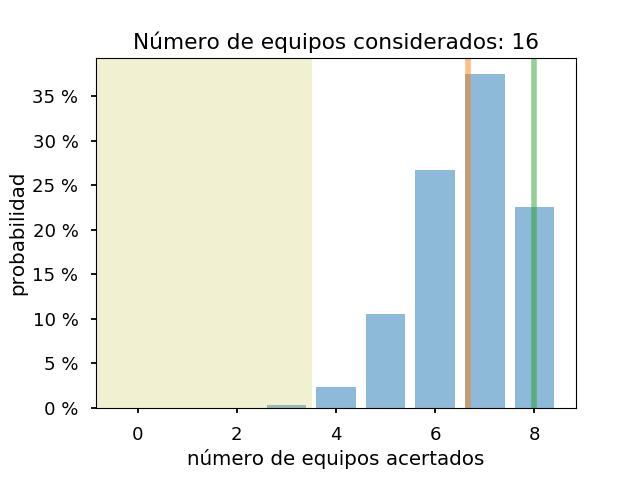
En todos los casos, el modelo considera que va a acertar un equipo de cuartos. Y el número de equipos acertados es bastante similar al real.
Con todas estas gráficas se muestra lo que se puede esperar del modelo. A mí no me parecen unos resultados espectaculares, así que la capacidad predictiva del modelo es limitada. Aunque por otra parte está claro que el modelo sí da la impresión de ser correcto y ser capaz de dar cierta información del resultado del partido, aunque información limitada. Que sea mejor o peor que lo que puede decir un analista deportivo, es otra cuestión que cada lector deberá valorar. Para ello pondré unas tablas donde se muestran todos los partidos: en verde, si el resultado coincide con el pronóstico; y si no coincide, en amarillo el resultado real y en rojo el pronóstico.


