Muestras de las encuestas y márgenes de error

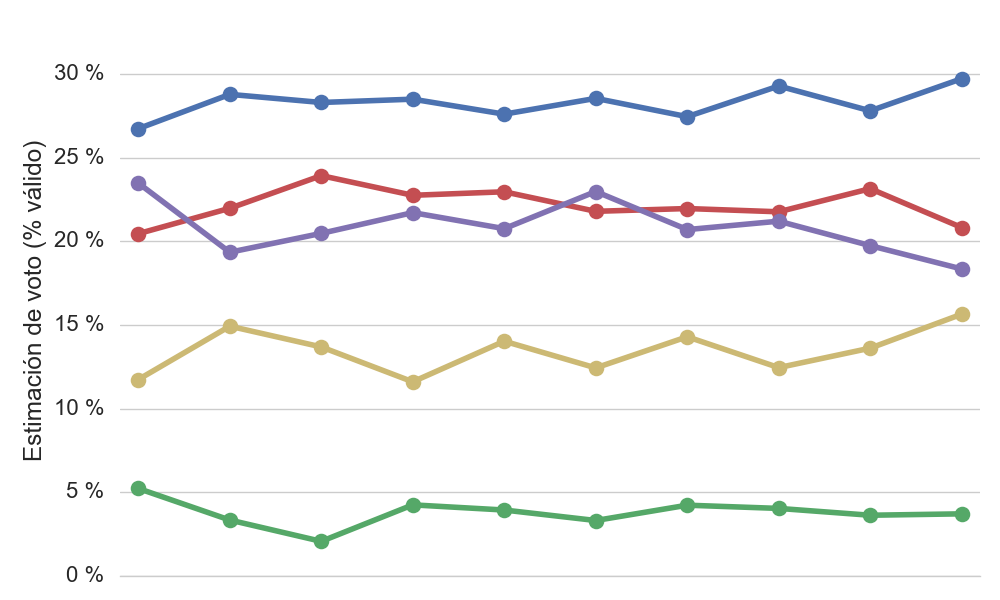
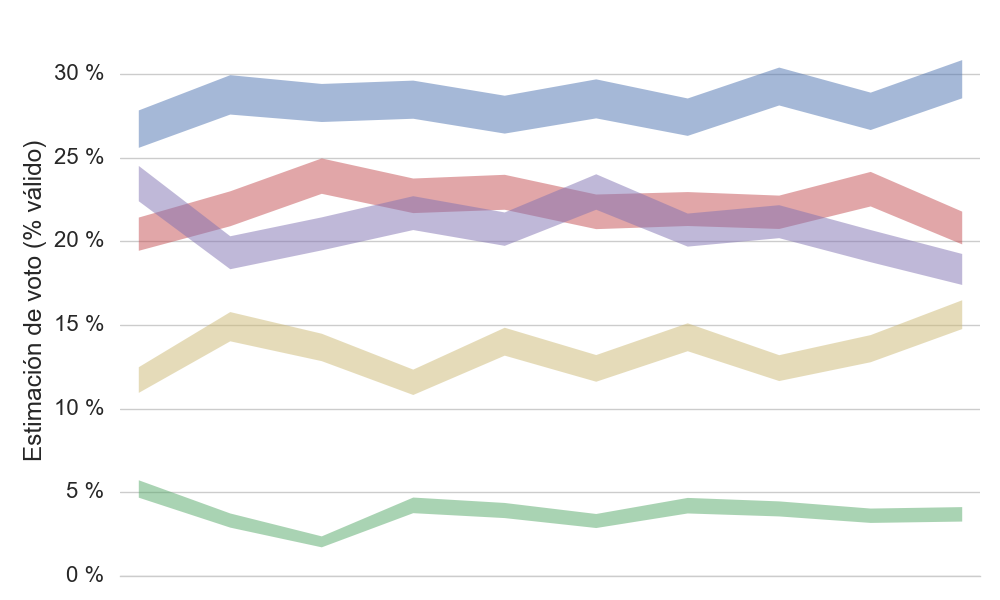
Esta gráfica enseña una serie de encuestas de intención de voto con muestras de 1.200 personas en un país que bien pudiera ser España, por decir uno cualquiera. ¿Te resulta familiar? Piensa un momento en qué conclusiones podrías sacar del análisis de la evolución de la intención de voto que indica la gráfica.

Se podría decir que el partido rojo y morado tienen una competición muy fuerte, y que en algunos momentos el partido morado sobrepasa al rojo en intención de voto. También se podría decir que al final la intención de voto del partido rojo y morado caen y asciende la del partido amarillo. Análisis parecidos se leen normalmente en los medios tras la publicación de una encuesta.

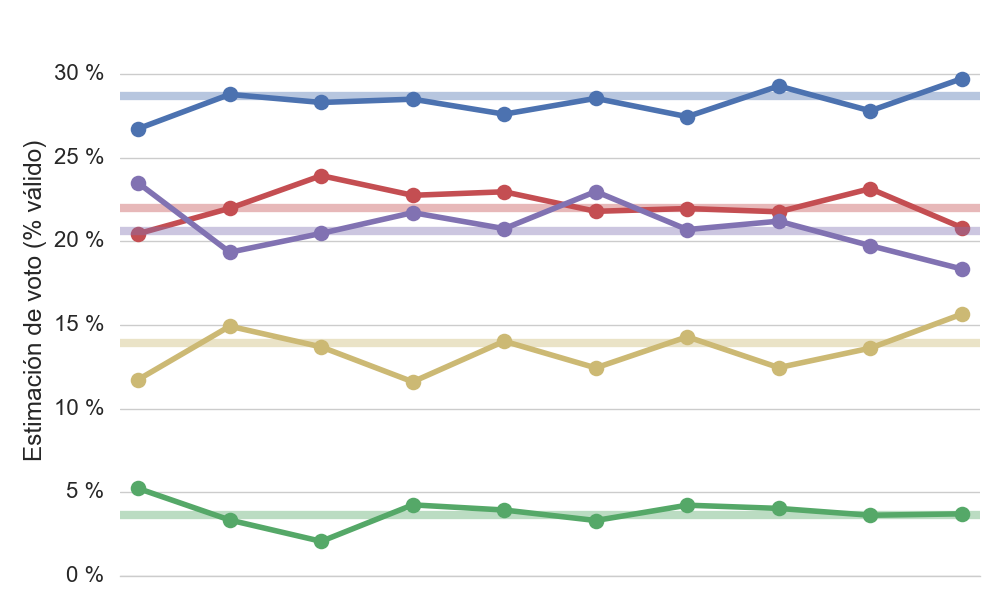
Sin embargo la gráfica aquí mostrada está generada a partir de una simulación de encuestas donde el porcentaje de voto de cada partido en la población total es estacionaria, no cambia, y las variaciones de la intención de voto son debidas solo a las fluctuaciones estadísticas, sin errores debidos a una cocina electoral o a una muestra sesgada. En la siguiente gráfica se muestran las intenciones de voto calculadas por las encuestas comparadas con el porcentaje real de cada partido (líneas horizontales del mismo color), valores que se han elegido inspirados en el resultado de las últimas elecciones generales:

En una encuesta de 1.200 entrevistas, el margen de error es de unos ±3 %, como se puede ver en la ficha técnica de las encuestas habituales: las encuestas no suelen sobrepasar las 1.200 entrevistas, salvo las del CIS.

El margen de error de una encuesta es la diferencia que debe tenerse en cuenta para el valor estimado sobre el censo para tener una confianza al 95 % de que la estimación es correcta, suponiendo que el resultado está alrededor del 50 %. Es decir, que si el margen de error es ±3 %, y el partido tiene una estimación del 50 % del censo, solo se puede decir que su resultado real estará entre 47 % y 53 % para estar seguros al 95 %. Normalmente en una encuesta, los partidos tienen estimaciones que no están cerca del 50 %, por lo que su margen de error será algo menor. Pero también, las estimaciones se dan en función del voto válido, lo que hace que el margen de error real se incremente. En la siguiente gráfica se muestra la distribución de resultados del partido morado según un montón de encuestas de 1.2oo entrevistas, siendo el porcentaje real del partido morado constante:

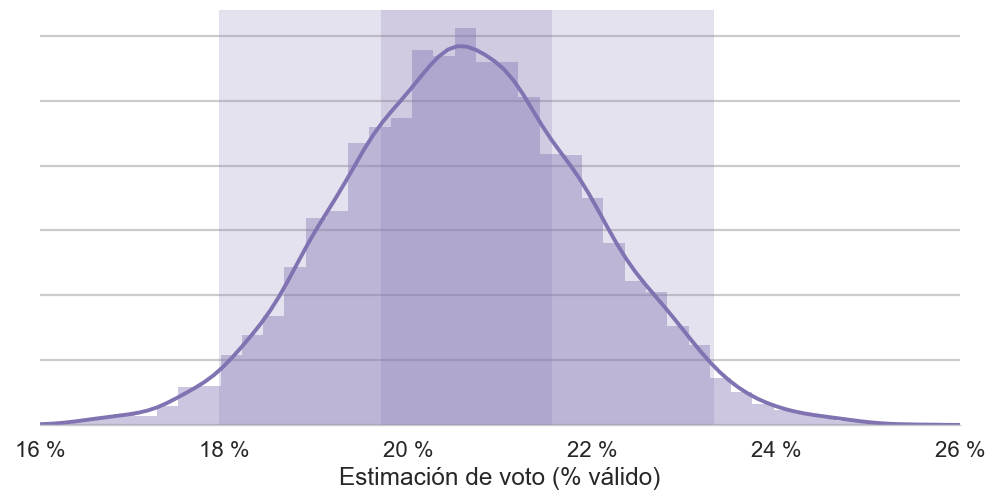
El voto en el país del partido morado es 20,6 %, pero debido a que las encuestas se hacen con muestras aleatorias limitadas a 1.200 personas, su resultado muestra una distribución. Las áreas rectangulares resaltadas muestran en rango que es necesario para incluir el 95 % de las estimaciones (la parte más clara, de 18 % hasta 23 %) y el 50 % (más oscura, de 20 % a 21,5 %). No hay forma estadística de evitar esta distribución, y si el conjunto de las muestras no muestra esta distribución es porque o las encuestas son falsas o porque la cocina se hace de forma que intenta evitar estas variaciones, con lo cual se está manipulando de forma inapropiada la naturaleza de encuesta.

En el siguiente gráfico se muestra cómo quedaría la primera gráfica de la evolución de la intención de voto si se dibujara el margen error de cada estimación de voto:

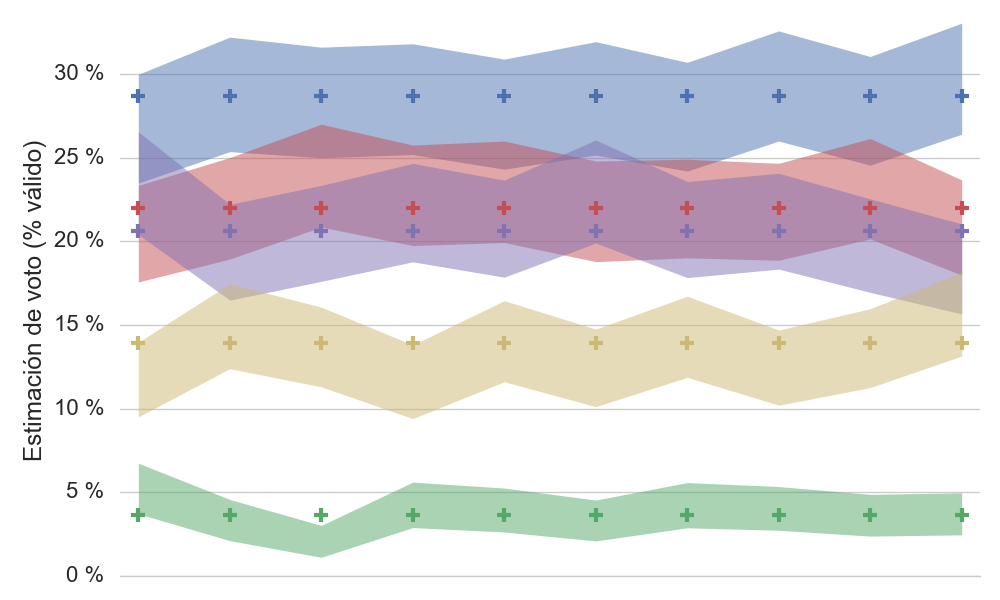
Se ve ahora que todo está más confuso, que los valores se superponen y que una diferencia de partidos del 1-2 % no es distinguible con muestras de 1.200 personas.

Si se dibuja el margen de error, en vez de con confianza al 95 % con confianza al 50 %, el gráfico es así:

Que las curvas representen la confianza al 50 % quiere decir que hay un 50 % de posibilidades de que el resultado real no esté dentro del área coloreada. Se confirma así que una diferencia del 1-2 % entre dos partidos es indistinguible estadísticamente. Para distinguirlos, harían falta encuestas con muestras mayores o que diferentes encuestas realizadas en las mismas fechas muestren resultados compatibles. No sirven encuestas realizadas en fechas diferentes, ya que entonces no se podría saber si es una fluctuación estadística o es que el sentido del voto de la población ha cambiado.

Debido a que la selección de muestras no es completamente aleatoria, para calcular el margen de error real también se debería tener en cuenta las diferentes muestras que se disponen en cada segmento de población.

Además de los márgenes de errores debidos a las fluctuaciones estadísticas, una estimación de una encuesta debería indicar márgenes de error debido a que está usando un modelo con suposiciones más o menos arbitrarias. Así en el estudio publicado por El Español, había hasta otro ±1,2 % extra de variación de voto achacable a usar un modelo u otro.

Desgraciadamente, la ficha técnica de las encuestas solo proporciona el margen de error de las fluctuaciones estadísticas, que solo es un límite inferior del margen de error real de la estimación de la encuesta.

En definitiva, quiero resaltar son dos cosas:

— Una diferencia del 2 % entre dos partidos no se puede diferenciar con las encuestas que habitualmente se publican.

— Las estimaciones del voto de una serie de encuestas deberían variar ±3 % aún en una situación estacionaria de voto. Variaciones de ese orden son compatibles con que el voto no haya cambiado. Que no haya variaciones, indicaría que se está utilizando la cocina para evitar o amortiguar esas variaciones, por ejemplo al promediar las nuevas estimaciones con las antiguas, desvirtuando en alguna forma el significado estadístico de una encuesta.